标题:Distributed Consensus-Based K-Means Algorithm in switching multi-agent networks
作者:LIN Peng ·WANG Yinghui ·QI Hongsheng ·HONG Yiguang
机构:Journal of Systems Science and Complexity volume
引用:Lin P, Wang Y, Qi H, et al. Distributed consensus-based k-means algorithm in switching multi-Agent networks[J]. Journal of Systems Science and Complexity, 2018, 31: 1128-1145.
研究问题Research Question
科学问题Science Question
- 许多聚类算法,如等,基本上都是集中式的。然而,快速增多的数据和大规模网络所带来的挑战,使得不得不在网络上的不同智能体之间存储和处理数据。例如,在网络监控、无线传感器网络或分布式数据库中,数据便是分布在网络上的。
研究核心Core of the research
-
本文讨论了在交换式多智能体网络中基于算法的分布式聚类设计,适用于数据分散存储且数据无法被所有智能体都获得的情况。
-
作者提出了一种分布式情况下基于共识的算法,即基于双时钟共识的算法()。
-
在温和的连接条件下,作者证明了的收敛性,以保证聚类问题的分布式解决方案,即使网络拓扑结构是时变的。
研究意义Research significance
-
由于可扩展性、鲁棒性和低成本性,多智能体网络中的分布式算法近年来备受关注。但智能体很难在大规模网络中直接获取所有信息,网络中的每个智能体只能基于与邻居之间的信息交换或局部测量来实现全局目标。为了保证所有智能体都为同一个目标工作,基于共识的算法在分布式控制、估计和优化领域得到了普及。
-
网络连通性在实现多智能体协调和使分布式算法/方法适合或有效处理大数据或复杂网络结构方面发挥着至关重要的作用。
-
近年来,机器学习由于在知识发现、模式识别和数据挖掘中的各种应用引起了越来越多的研究关注。 数据聚类是用于数据分析的无监督机器学习问题之一,自从提出有效地将数据划分为小的集群以来,它也被大量研究并广泛应用于许多领域。基于数据之间的相似性,分区聚类算法(与分层算法相反)成为重要的研究课题,部分原因是这些算法可以同步获得所有聚类,而不需要分层结构。例如,算法是最流行的分区聚类算法之一,以其简单性和快速收敛速度而闻名。
现有算法的不足Shortcomings of existing algorithm
- 大多数现有的分布式 算法都是针对固定拓扑提出的,并且是在仿真的基础上进行分析,该类算法在链路故障或交换网络连接的情况下可能会失败。
结论Conclusion
-
本文讨论了多智能体网络的聚类问题,并针对数据存储在不同智能体或所有智能体不可用的情况,提供了一种全分布式算法。
-
作者提出了一种基于双时钟共识的聚类算法()来解决聚类问题,通过使智能体在没有全局信息的情况下在共同连接的拓扑结构上达成共识。此外,作者还给出了该算法的收敛性分析,并通过使用各种真实的聚类数据集提供实例,以证明所提出的分布式算法的有效性。
理论与方法Theory and Method
图论
-
,表示一个在个智能体之间共享拓扑的图
-
,表示智能体的集合
-
,表示智能体之间的通信链路的集合
-
如果智能体可以直接从智能体接收信息,则存在从到的有向边,记为
-
将智能体的一度邻居表示为
-
若且,则称图为无向图
-
-
-
一条长度为的有向路径是一个非空图 ,形式为 ,,其中都是不同的
-
如果对于任意对,图存在有向边,则称图是强连通的
-
图表示在时间上智能体之间的时变通信拓扑,的邻接矩阵记为,其元素定义如下:
-
,表示,同时也包括智能体本身即
-
,表示智能体没有与智能体直接连通
-
集中式聚类
-
集中式算法()是一种两步骤(分配步骤和细化步骤)的迭代方法。
-
用表示时间时的个中心点,集中式聚类算法通过个随机中心点或仅有一个随机中心点的算法来进行。
-
在划分步骤中,每个数据点被分配到可以由最近的中心点代表的聚类中,即
换句话说,即
和分别代表了数据点的大小和数据点的总和,这些数据点在时间时属于第个集群。
为了简单起见,定义:
-
在细化步骤中,个中心点被每个集群中的新中心点所更新,即
-
集中式聚类算法保证了获得局部最优解。
-
在集中式聚类算法中,算法需要得知全局或集中的信息。
但如果数据点在空间上分布或有不同的智能体收集,集中式的形式可能就不再适用了。
假设
时变网络又称为联合连通网络
假设一
-
假设图的加权邻接矩阵满足:
-
是双随机的
随机矩阵:每一项均为非负的并且每行的和均为1的方阵
双随机矩阵:每一列的和均为1的随机矩阵 -
对于所有的 ,有 且 ,其中 是一个正标量
-
假设二
-
若图是联合连通的,则对于所有的和某个整数是强连通的
-
该假设确保了尽管网络拓扑正在切换并且可能不会在每个时刻都连接,每个代理在每个周期内至少可以从所有邻居那获取信息一次,
-
在以上两个假设的前提下,对于所有的和所有的,有
-
其中,,是一个由定义的转移概率矩阵,
转移概率矩阵(跃迁矩阵)
-
定义:矩阵各元素都是非负的,且各行元素值和为1,各元素用概率表示,在一定条件下是互相转移的。表示步转移概率矩阵
-
特征:
-
-
,即矩阵中每一行的转移概率之和为1
-
-
有转移概率组成的矩阵称为转移概率矩阵,即构成转移概率矩阵的元素是转移概率
马尔可夫过程
-
马尔可夫性(无后效性)
在过程或系统在时刻所处的状态为已知的条件下,过程在时刻所处状态的条件分布,与过程在时刻之前的状态无关的特性
即过程“将来”的情况与“过去”的情况是无关的
-
马尔可夫过程的定义
具有马尔可夫性的随机过程称为马尔可夫过程
用分布函数表述马尔可夫过程:
待补充……
-
分布式聚类
相关说明
-
对于每个智能体,训练集是可获得的,其中,是数据的维度,是数据的大小,为整个数据集。
-
智能体的目的是根据的聚类准则将数据集划分成个集群。
-
智能体所获得的表示集群的个中心点可能并不属于数据集。
-
令表示第个质心,是个中心点的集合。
-
智能体的聚类问题,可表述如下:
其中,
而,且数据点之间的相似性通过欧几里得范数来衡量
L1范数:向量中各个元素绝对值之和
L2范数(欧几里得范数/欧氏距离/L2距离):向量元素的平方和再开方
-
在分布式聚类学习中,智能体的目的是将数据集划分成个集群 并且最小化数据点和聚类中心点之间的距离平方和
-
所有智能体所得到的个中心点应该是相互一致的(不太懂是什么意思)
-
分布式聚类问题,可表达如下:
-
假设每个智能体都“知道”值,若未知,则可使用文献[31]中提出的方法来估计值
基于双时钟共识的K-Means算法
-
为了解决问题(4),定义为中心点的集合,这些中心点是由智能体在时间获得的。根据集中式聚类算法,给定,可以通过以下公式进行分配
即
显然,代表在时间的第个集群中属于智能体的数据大小,表示为
设作为的集合,那么一个新的局部求和可以通过以下方式得到
因此,全局中心点被重写如下:
表示为,其中,
在算法的每次迭代中,智能体通过以下三个步骤更新其中心点:
-
本地步骤
智能体根据(9)、(10)和(11)分别计算、和。
-
共识步骤
在一个信息共享拓扑上,该拓扑是随时间变化的,并满足假设2.1和2.2,代理根据以下公式与它的一度邻居交换信息,直到达成共识
在共同连接的拓扑结构上,共识步骤的停止时间用表示。
-
本地更新步骤
智能体根据以下方式更新:
-
-
综上,基于双时钟共识的算法()的伪代码如下所示:

-
与现有的算法不同,有两个时钟。
在共识步骤中,智能体与它的一度邻居智能体交换信息,直到在某个容许范围内达成共识,这对于固定时间的本地步骤的时钟很容易实现,并且可以适应全局通信拓扑不可用的情况。
-
即使链路故障/恢复程序或节能政策导致网络拓扑联合连接地切换,共识步骤中的共识率仍然是指数级的。
DCKA的收敛性分析
-
假设,其中
由(12)中的的定义可得,,
定义如下:
即为智能体在共识步骤的时间对的估计
-
鉴于可以获得局部最优解,如果能够首先证明当s → ∞时,收敛于,然后证明存在一个,使得和之间的误差对没有影响,那么结论就成立了。证明如下:
-
证明当时,收敛于。
对于所有的。有
设
由于在假设2.1和2.2的前提下,实现了分布式聚类问题(4)的局部最优解,可得:
因此
表示为
根据(18)可得
因此,对于任意,存在一个,对于任意的,有
其中,。换句话说,当s→S时,收敛于。
-
证明和之间的误差对没有影响。
因为是由每个集群的中心点决定的,所以将 表示为 。若给定中心点 ,取
其中,
对于任意的,有,其中
对于,如果选择,其中
则对于所有和,有
换句话说,如果,有。因此,和在下一次迭代中应该得到相同的,即和之间的误差对没有影响。
-
DCKA的通信和计算复杂性分析
-
定义为的最大迭代次数,为所有智能体中数据点的总数,为通信网络中的平均链接数。
-
当通信网络的拓扑结构被假定为联合连接时,可以比网络全程保持连接时小很多。
-
通信复杂性
-
的通信复杂性与集群、迭代、网络链接等密切相关。在的一个循环共识步骤中,每个智能体向其一度邻居发送关于集群的。
-
用表示发送的字节数,则在个循环中,通信消耗为2。因此,总的通信消耗为。
-
-
计算复杂性
-
的时间复杂度取决于数据集的大小、网络中智能体的数量、集群的数量以及相关的因素。
-
网络中的智能体需要大小为的空间来存储个中心点,大小为的空间来存储的值,大小为的空间用于共识步骤。因此,总的空间复杂性为。
-
每次迭代,本地步骤的时间复杂度为,共识步骤为,本地更新步骤为。因此,的总时间复杂度为。此外,当数据集的大小非常大时,的总时间复杂性为。
-
在中,所考虑的网络中的智能体与它们的一度邻居分享它们的信息以获得相同的中心点。由于所有智能体中所有中心点的共识和中心点的更新完全分开,继承了的收敛率。智能体之间的通信拓扑结构被假定为联合连接的。网络中的每个智能体在每个期间至少与它的一度邻居通信一次。联合连接适用于智能体之间链接的故障,也适用于通信成本的降低。
实验Experiment
实验一
-
该实验基于一个合成数据集,其中聚类数据对应于二维空间中的个不同的高斯分布。
-
假设这9个不同的高斯分布具有不同的平均值,分别用 , 和 表示,它们共享相同的协方差矩阵 ,其中 是一个二维的特征矩阵。
-
假设网络中有五个智能体。每个智能体都可以访问一个大小为900的部分数据集,每个高斯分布有100个数据点,这些数据都是随机生成的。
-
每个智能体的目标是用部分数据集找到相同的九个集群中心点。为了衡量所提出的算法的聚类性能,距离的平方之和()定义如下:
其中,。智能体的初始聚类中心点, 是从部分数据集中随机选择的。
-
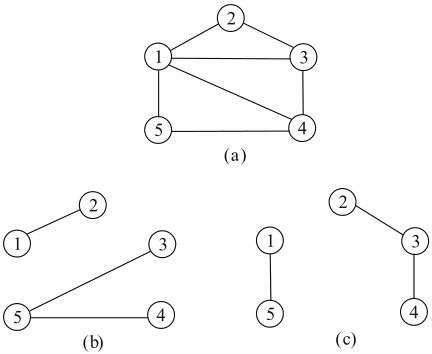
在中,假设通信拓扑结构是联合连接的。在时间时,通信拓扑结构假定为图(b),在时间时,为图 ( c ) ,。
-
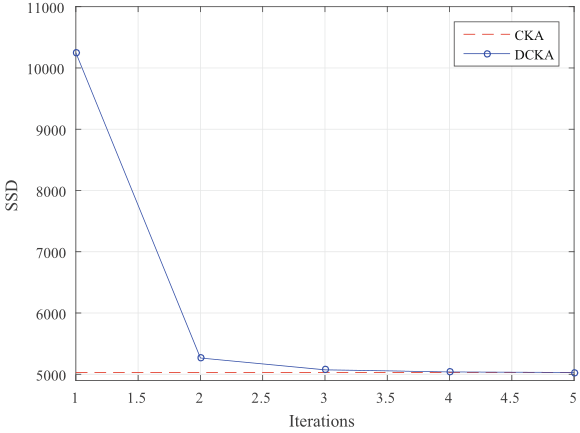
首先,研究了与相比的,结果如下图所示。结果表明两种算法的是一样的,都是5028.54。
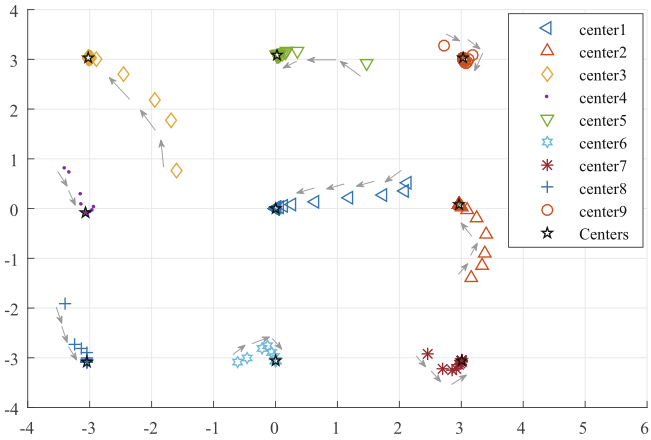
下图更直观地显示了聚类的结果,中心点 , , 。图中的五边形是由 得到的中心点,其它的则是由 得到的中心点。下图表明,尽管智能体之间的通信拓扑结构发生了变化,但 的表现与一样好。
-
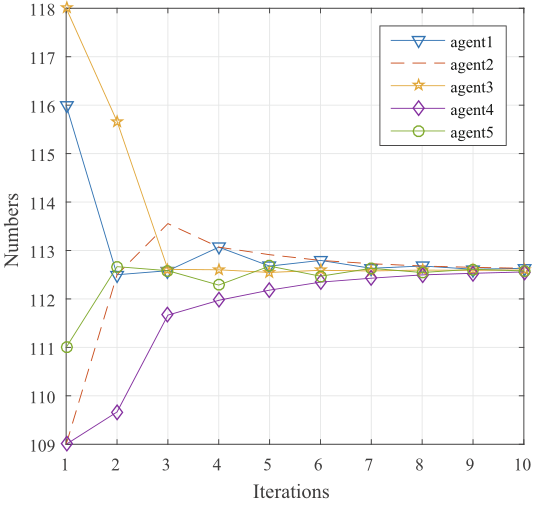
接下来,研究所提出的算法的共识性能。下图显示了每个智能体的的性能。可以发现,在共识步骤中,可以快速达到。事实上,收敛率是指数级的。
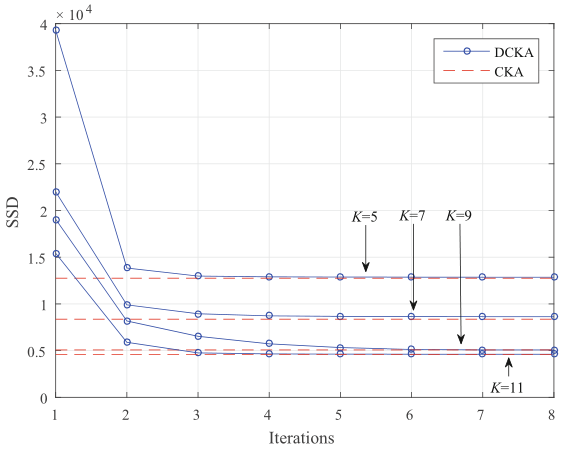
考虑在不同的值下的行为,如下图所示,尽管值不同,但的表现仍与一样好。
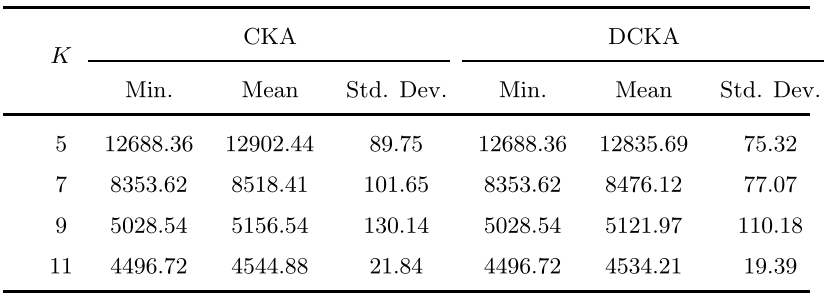
由于和的聚类结果都与初始中心点的选择有关,因此为了测试算法,模拟了100次不同值的蒙特卡洛运行。其结果如下图显示。由下图可知,和都有相同的最小。然而,由于初始中心点的多样性,在的平均值和标准偏差上优于。这是因为必须用个中心点随机初始化,而对于,每个智能体是根据它们的部分数据集,用个中心点进行初始化。 因此,通常可以得到比更好的结果。
-
最后,研究了与算法相比的通信和计算消耗。
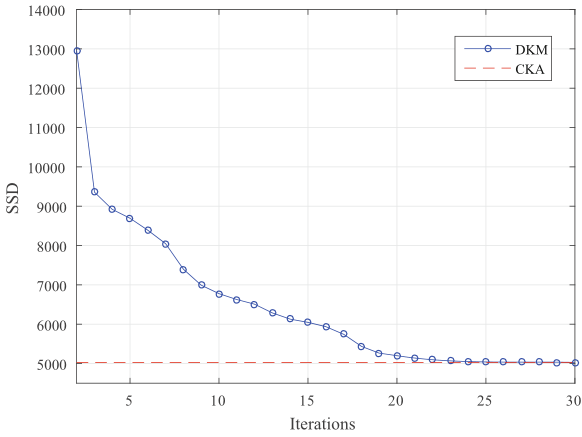
在通信拓扑结构选择为(a)的情况下,算法也可以应用于解决聚类问题。下图显示了时的值,其中,中的参数被假定为。在中,大约需要30次迭代来完成聚类任务,其收敛速度很慢,智能体需要与它们的邻居通信30次左右,总的通信消耗为210。然而,的通信成本只有大约150,比的通信成本低得多。尽管如此,网络中算法的智能体仍需要对4500个数据点进行约30次处理,而的代理只需要对整个数据集进行约5次处理。
-
实验二
-
在本实验中,选择了、和作为实验数据集。每个数据集由100000个实体组成,这些实体都是二维向量,真实聚类数都是。考虑一个有20个智能体的网络。对于,每个智能体可以随机获得5000个数据点,形成自己的部分数据集,而则是在整个数据集 上进行。
-
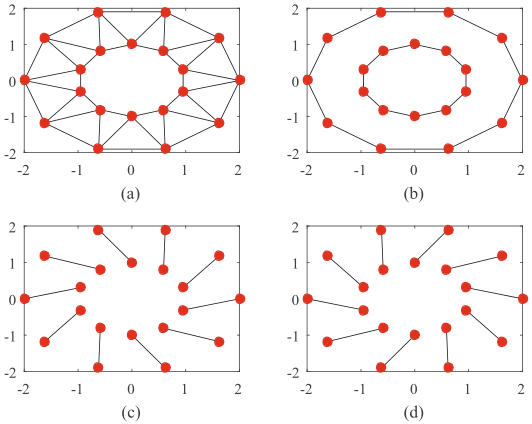
在中,假设智能体的时间变化的通信拓扑是联合连通的。在时间和 ,时,拓扑结构分别如下图(b)、(c)、(d)所示,而(a)图为它们的联合。
-
作者模拟了60次不同值的蒙特卡洛运行,以测试两种算法在这些数据集上的性能,其结果分别如下图所示。在这三个数据集中,在的平均值和标准差上都优于,而当和100时,只在的最小值上优于。结果显示,与相比,对初始化不那么敏感,通常可以得到很好的结果。
在上运行60次蒙特卡洛的结果:
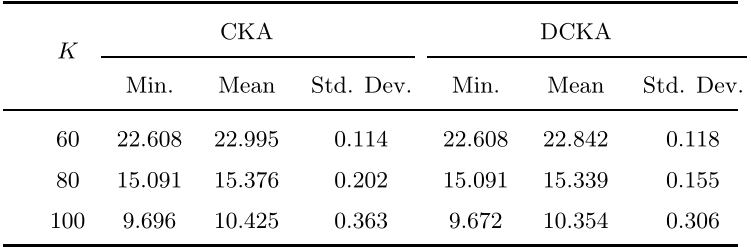
在上运行60次蒙特卡洛的结果:
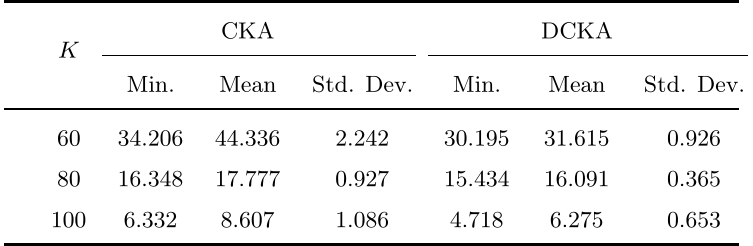
在上运行60次蒙特卡洛的结果: