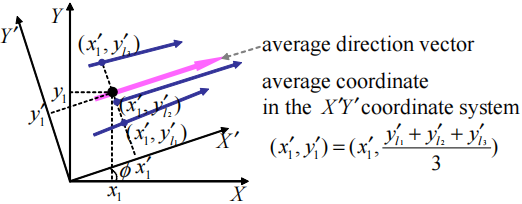标题:Trajectory Clustering: A Partition-and-Group Framework
研究问题Research Question
科学问题Science Question
研究核心Core of the research
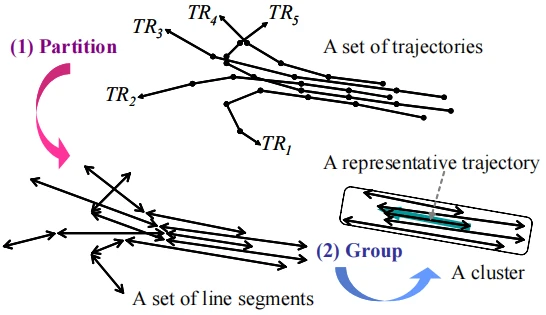
基于分区和分组架构(将轨迹划分为一组线段,然后将相似的轨迹聚为一个类)的轨迹聚类算法,整体过程如下图:
首先,每个轨迹被划分成一组线段;
其次,根据距离度量,彼此接近的线段被分组成一个簇;
最后,为每个簇生成一个有代表性的轨迹;
研究意义Research significance
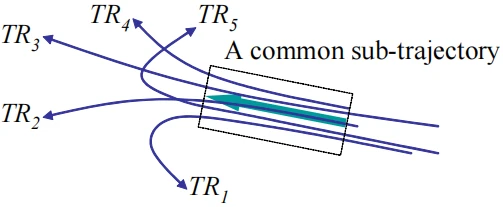
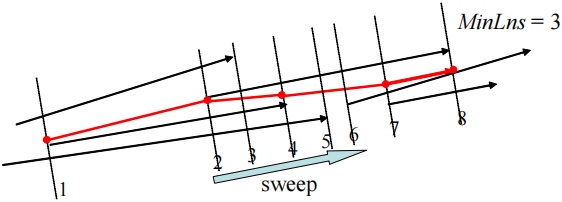
考虑下图中的五个轨迹,可以发现,在虚线矩形中五条轨迹有一个共同的行为(用粗箭头表示)。然而,如果把这些轨迹以一个整体进行聚类,则无法发现其共同的行为,因为它们向完全不同的方向移动,因此将错过一些有价值的信息。共同子轨迹的实际应用价值 :
飓风的登陆预报
道路和交通对动物运动的影响
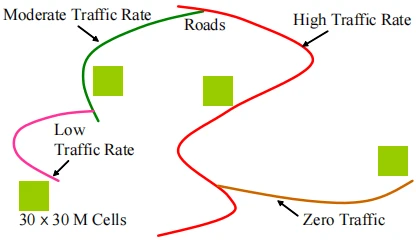
考虑下图中的动物栖息地和道路(粗线代表道路,且它们有着不同的交通速率)。Wisdom等人探讨了骡鹿和麋鹿与不同交通速率的道路之间的空间格局。更具体地说,其中一个目标是评估骡鹿和麋鹿避开道路附近地区的程度(这些区域用实心矩形表示)。因此,本文提出的框架对这类研究确实很有用。
现有算法的不足Shortcomings of existing algorithm
现有算法将相似的轨迹作为一个整体进行分组,从而发现相似的轨迹,但可能会错过常见的子轨迹。
结论Conclusion
基于分区和分组架构,开发了一轨迹聚类算法,该算法包括以下两个阶段:
分区阶段 ——每个轨迹都被最优地划分为一组线段,这些线段将被提供给下一阶段M D L MDL M D L 分组阶段 ——将类似的线段分组为一个集群
本文提出了一基于密度的线段聚类算法。
基于密度的聚类方法是最适合用于线段的,因为它们可以发现任意形状的聚类,并可以过滤出噪声。
线段簇通常是任意形状的,且轨迹数据库通常包含大量的噪声(即异常值)。
结果表明,从真实轨迹数据中发现了常见的子轨迹。
理论与方法Theory and Method
距离函数
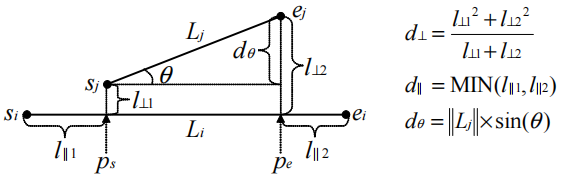
三个组成部分:垂直距离d ⊥ d_{⊥} d ⊥ d k d_{k} d k d θ d_{\theta} d θ
假设:L i = s i e i L_{i} = s_{i}e_{i} L i = s i e i L j = s j e j L_{j} = s_{j}e_{j} L j = s j e j d d d s i , e i , s j 和 e j s_{i},\ e_{i},\ s_{j}和e_{j} s i , e i , s j 和 e j d d d L i ≥ L j L_{i}≥L_{j} L i ≥ L j
垂直距离 d ⊥ ( L i , L j ) = l ⊥ 1 2 + l ⊥ 2 2 l ⊥ 1 + l ⊥ 2 d_{\perp}\left(L_{i}, L_{j}\right)=\frac{l_{\perp 1}^{2}+l_{\perp 2}^{2}}{l_{\perp 1}+l_{\perp 2}} d ⊥ ( L i , L j ) = l ⊥ 1 + l ⊥ 2 l ⊥ 1 2 + l ⊥ 2 2 s j 和 e j s_{j}和e_{j} s j 和 e j L i L_{i} L i p s 和 p e p_{s}和p_{e} p s 和 p e l ⊥ 1 l_{⊥1} l ⊥1 s j s_{j} s j p s p_{s} p s l ⊥ 2 l_{⊥2} l ⊥2 e j e_{j} e j p e p_{e} p e 平行距离 d ∥ ( L i , L j ) = MIN ( l ∥ 1 , l ∥ 2 ) d_{\|}\left(L_{i}, L_{j}\right)=\operatorname{MIN}\left(l_{\| 1}, l_{\| 2}\right) d ∥ ( L i , L j ) = MIN ( l ∥1 , l ∥2 ) s j s_{j} s j e j e_{j} e j L i L_{i} L i p s p_{s} p s p e p_{e} p e l ∥ 1 l_{\| 1} l ∥1 p s p_{s} p s s i s_{i} s i e i e_{i} e i l ∥ 2 l_{\| 2} l ∥2 p e p_{e} p e s i s_{i} s i e i e_{i} e i M A X ( l ∥ 1 , l ∥ 2 ) MAX(l_{\| 1},l_{\| 2}) M A X ( l ∥1 , l ∥2 ) M I N ( l ∥ 1 , l ∥ 2 ) MIN(l_{\| 1},l_{\| 2}) M I N ( l ∥1 , l ∥2 ) 角距离 d θ ( L i , L j ) = { ∥ L j ∥ × sin ( θ ) , if 0 ∘ ≤ θ < 9 0 ∘ ∥ L j ∥ , if 9 0 ∘ ≤ θ ≤ 18 0 ∘ d_{\theta}\left(L_{i}, L_{j}\right)= \begin{cases}\left\|L_{j}\right\| \times \sin (\theta), & \text { if } 0^{\circ} \leq \theta<90^{\circ} \\ \left\|L_{j}\right\|, & \text { if } 90^{\circ} \leq \theta \leq 180^{\circ}\end{cases} d θ ( L i , L j ) = { ∥ L j ∥ × sin ( θ ) , ∥ L j ∥ , if 0 ∘ ≤ θ < 9 0 ∘ if 9 0 ∘ ≤ θ ≤ 18 0 ∘ ∥ L j ∥ \| L_{j}\| ∥ L j ∥ L j L_{j} L j θ \theta θ L i 和 L j L_{i}和L_{j} L i 和 L j ∥ k j ∥ × s i n ( θ ) \|k_{j}\|×sin(\theta) ∥ k j ∥ × s in ( θ ) 向量表示 a b → \overrightarrow{a b} ab a , b a,\ b a , b p s = s i + u 1 ⋅ s i e i → , p e = s i + u 2 ⋅ s i e i → p_{s}=s_{i}+u_{1} \cdot \overrightarrow{s_{i} e_{i}}, \quad p_{e}=s_{i}+u_{2} \cdot \overrightarrow{s_{i} e_{i}} p s = s i + u 1 ⋅ s i e i , p e = s i + u 2 ⋅ s i e i u 1 = s i s j → ⋅ s i e i → ∥ s i e i → ∥ 2 , u 2 = s i e j → ⋅ s i e i → ∥ s i e i → ∥ 2 u_{1}=\frac{\overrightarrow{s_{i} s_{j}} \cdot \overrightarrow{s_{i} e_{i}}}{\left\|\overrightarrow{s_{i} e_{i}}\right\|^{2}}, \quad u_{2}=\frac{\overrightarrow{s_{i} e_{j}} \cdot \overrightarrow{s_{i} e_{i}}}{\left\|\overrightarrow{s_{i} e_{i}}\right\|^{2}} u 1 = ∥ s i e i ∥ 2 s i s j ⋅ s i e i , u 2 = ∥ s i e i ∥ 2 s i e j ⋅ s i e i θ \theta θ cos ( θ ) = s i e i → ⋅ s j e j → ∥ s i e i → ∥ ∥ s j e j → ∥ \cos (\theta)=\frac{\overrightarrow{s_{i} e_{i}} \cdot \overrightarrow{s_{j} e_{j}}}{\left\|\overrightarrow{s_{i} e_{i}}\right\|\left\|\overrightarrow{s_{j} e_{j}}\right\|} cos ( θ ) = ∥ s i e i ∥ ∥ s j e j ∥ s i e i ⋅ s j e j 综上,两线段之间的距离定义为 ( L i , L j ) = w ⊥ ⋅ d ⊥ ( L i , L j ) + w ∥ ⋅ d ∥ ( L i , L j ) + w θ ⋅ d θ ( L i , L j ) (L_{i},L_{j}) = w_{⊥}·d_{⊥}(L_{i},\ L_{j})+w_{\|}·d_{\|}(L_{i},\ L_{j})+w_{\theta}·d_{\theta}(L_{i},\ L_{j}) ( L i , L j ) = w ⊥ ⋅ d ⊥ ( L i , L j ) + w ∥ ⋅ d ∥ ( L i , L j ) + w θ ⋅ d θ ( L i , L j ) w k 和 w θ w_{k}和w_{\theta} w k 和 w θ
轨迹划分
理想属性
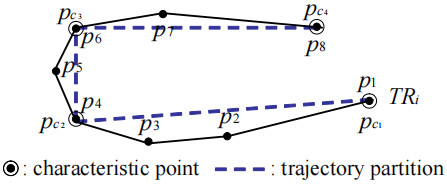
轨迹行为中快速变化的点,称之为特征点。T R i = p 1 p 2 p 3 ⋯ p j ⋯ p l e n i T R_{i}=p_{1} p_{2} p_{3} \cdots p_{j} \cdots p_{l e n_{i}} T R i = p 1 p 2 p 3 ⋯ p j ⋯ p l e n i { p c 1 , p c 2 , p c 3 , ⋯ , p c pari } \left\{p_{c_{1}}, p_{c_{2}}, p_{c_{3}}, \cdots, p_{c_{\text {pari }}}\right\} { p c 1 , p c 2 , p c 3 , ⋯ , p c pari } ( c 1 < c 2 < c 3 < ⋅ ⋅ ⋅ < c p a r i ) (c_{1}<c_{2}<c_{3}<···<c_{par_{i}}) ( c 1 < c 2 < c 3 < ⋅⋅⋅ < c p a r i ) T R i TR_{i} T R i T R i TR_{i} T R i p a r i par_{i} p a r i { p c 1 p c 2 , p c 2 p c 3 , ⋯ , p c p a r i − 1 p c p a r i } \left\{p_{c_{1}} p_{c_{2}}, p_{c_{2}} p_{c_{3}}, \cdots, p_{c_{p a r_{i}}-1} p_{c_{p a r_{i}}}\right\} { p c 1 p c 2 , p c 2 p c 3 , ⋯ , p c p a r i − 1 p c p a r i }
轨迹的最优划分应该具有两个理想的特性——精确性和简洁性,精确性意味着轨迹与其一组轨迹分区之间的差异应该尽可能小,简洁性意味着轨迹分区的数量应该尽可能少。
实验发现,实现精确性要求每一处轨迹分区其行为是迅速变化的。否则,就无法达到精确性。如在上图中若没有选择 p c 2 p_{c2} p c 2 T R i TR_{i} T R i p c 1 p c 3 p_{c1}\ p_{c3} p c 1 p c 3
精确性和简洁性是相互矛盾的。例如,如果选择一个轨迹中的所有点都作为特征点(即 p a r i = l e n i par_{i}=len_{i} p a r i = l e n i p a r i = 2 par_{i}=2 p a r i = 2
使用MDL原理进行形式化
M D L MDL M D L L ( H ) 和 L ( D ∣ H ) L(H)和L(D|H) L ( H ) 和 L ( D ∣ H ) H H H D D D H 和 D H和D H 和 D L ( H ) L(H) L ( H ) L ( D ∣ H ) L(D|H) L ( D ∣ H ) D D D H H H L ( H ) 和 L ( D ∣ H ) L(H)和L(D|H) L ( H ) 和 L ( D ∣ H ) 在轨迹划分问题中,一个假设对应于一组特定的轨迹划分。因此,找到最优划分可以转化为使用M D L MDL M D L
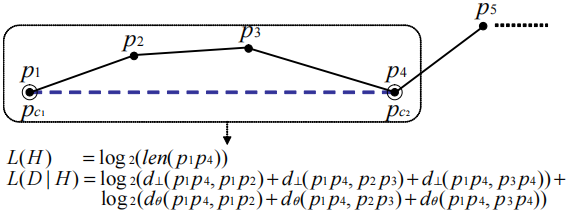
假设一个轨迹 T R i = p 1 p 2 p 3 ⋅ ⋅ ⋅ p j ⋅ ⋅ ⋅ p l e n i TR_{i}=p_{1}p_{2}p_{3}···p_{j}···p_{len_{i}} T R i = p 1 p 2 p 3 ⋅⋅⋅ p j ⋅⋅⋅ p l e n i = p c 1 、 p c 2 、 p c 3 、 ⋅ ⋅ ⋅ 、 p c p a r i ={p_{c1}、p_{c2}、p_{c3}、···、p_{c_{par_{i}}}} = p c 1 、 p c 2 、 p c 3 、 ⋅⋅⋅ 、 p c p a r i
L ( H ) = ∑ j = 1 p a r i − 1 log 2 ( len ( p c j p c j + 1 ) ) L(H)=\sum_{j=1}^{p a r_{i}-1} \log _{2}\left(\operatorname{len}\left(p_{c_{j}} p_{c_{j+1}}\right)\right) L ( H ) = ∑ j = 1 p a r i − 1 log 2 ( len ( p c j p c j + 1 ) ) l e n ( p c j p c j + 1 ) len(p_{c_{j}}p_{c_{j+1}}) l e n ( p c j p c j + 1 ) p c j p c j + 1 p_{c_{j}}p_{c_{j+1}} p c j p c j + 1 p c j p_{c_{j}} p c j p c j + 1 p_{c_{j+1}} p c j + 1 L ( H ) L(H) L ( H ) L ( D ∣ H ) = ∑ j = 1 p a r i − 1 ∑ k = c j c j + 1 − 1 { log 2 ( d ⊥ ( p c j p c j + 1 , p k p k + 1 ) ) + log 2 ( d θ ( p c j p c j + 1 , p k p k + 1 ) ) } L(D \mid H)=\sum_{j=1}^{p a r_{i}-1} \sum_{k=c_{j}}^{c_{j+1}-1}\left\{\log _{2}\left(d_{\perp}\left(p_{c_{j}} p_{c_{j+1}}, p_{k} p_{k+1}\right)\right)+\log _{2}\left(d_{\theta}\left(p_{c_{j}} p_{c_{j+1}}, p_{k} p_{k+1}\right)\right)\}\right. L ( D ∣ H ) = ∑ j = 1 p a r i − 1 ∑ k = c j c j + 1 − 1 { log 2 ( d ⊥ ( p c j p c j + 1 , p k p k + 1 ) ) + log 2 ( d θ ( p c j p c j + 1 , p k p k + 1 ) ) } L ( D ∣ H ) L(D|H) L ( D ∣ H ) p c j p c j + 1 p_{c_{j}}p_{c_{j+1}} p c j p c j + 1 p k p k + 1 ( c j ≤ k ≤ c j + 1 − 1 ) p_{k}p_{k+1}(c_{j}≤k≤c_{j+1}−1) p k p k + 1 ( c j ≤ k ≤ c j + 1 − 1 )
长度和距离都是实数。在实践中,对实数 x x x δ δ δ x δ x_{δ} x δ ∣ x − x δ ∣ < δ |x−x_{δ}|<δ ∣ x − x δ ∣ < δ x x x x ≈ x δ x≈x_{δ} x ≈ x δ L ( x ) = l o g 2 x − l o g 2 δ L(x)=log_{2}x−log_{2}δ L ( x ) = l o g 2 x − l o g 2 δ δ δ δ L ( x ) L(x) L ( x ) l o g 2 x log_{2}x l o g 2 x
线段的长度而不是线段的端点来定义L ( H ) L(H) L ( H )
首先,我们的任务是根据线段(子轨迹)的相对距离对它们进行聚类。长度(反映在L ( H ) L(H) L ( H ) L ( D ∣ H ) L(D|H) L ( D ∣ H )
其次,不使用端点的一个非常重要的原因是为了使聚类结果不受线段的坐标值的影响。也就是说,一堆线段可以从低坐标位置移动到高坐标位置,但距离函数应该仍然能够正确地测量相对距离。如果用两个端点的坐标值来表示L ( H ) L(H) L ( H )
注意到,L ( H ) L(H) L ( H ) L ( D ∣ H ) L(D|H) L ( D ∣ H ) L ( H ) L(H) L ( H ) L ( D ∣ H ) L(D|H) L ( D ∣ H )
如前所述,需要找到使L ( H ) + L ( D ∣ H ) L(H)+L(D|H) L ( H ) + L ( D ∣ H )
近似解
关键思想是将局部最优的集合视为全局最优
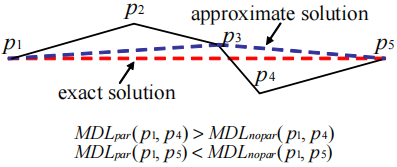
M D L c o s t = L ( H ) + L ( D ∣ H ) MDL\ cost =L(H)+L(D|H) M D L cos t = L ( H ) + L ( D ∣ H ) 设 M D L p a r ( p i , p j ) MDL_{par}(p_{i}, p_{j}) M D L p a r ( p i , p j ) p i p_{i} p i p j p_{j} p j p i p_{i} p i p j ( i < j ) p_{j}(i<j) p j ( i < j ) M D L c o s t MDL\ cost M D L cos t M D L n o p a r ( p i , p j ) MDL_{nopar}(p_{i}, p_{j}) M D L n o p a r ( p i , p j ) p i p_{i} p i p j p_{j} p j M D L c o s t MDL\ cost M D L cos t
M D L n o p a r ( p i , p j ) MDL_{nopar}(p_{i}, p_{j}) M D L n o p a r ( p i , p j ) L ( D ∣ H ) L(D|H) L ( D ∣ H ) k k k M D L p a r ( p i , p k ) ≤ M D L n o p a r ( p i , p k ) MDL_{par}(p_{i},p_{k})≤MDL_{nopar}(p_{i},p_{k}) M D L p a r ( p i , p k ) ≤ M D L n o p a r ( p i , p k ) p i p k p_{i}p_{k} p i p k i < k ≤ j i<k≤j i < k ≤ j p k p_{k} p k M D L c o s t MDL\ cost M D L cos t 下图显示了近似轨迹划分算法。M D L p a r MDLpar M D L p a r M D L n o p a r MDLnopar M D L n o p a r M D L p a r MDLpar M D L p a r M D L n o p a r MDLnopar M D L n o p a r p c u r r I n d e x − 1 p_{currIndex−1} p c u rr I n d e x − 1 C P i CP_{i} C P i
定理1 。上图中算法的时间复杂度为 O ( n ) O(n) O ( n ) n n n T R i TR_{i} T R i M D L MDL M D L T R i TR_{i} T R i n − 1 n−1 n − 1 当然,该算法可能无法找到最优的分区。M D L c o s t MDL\ cost M D L cos t { p 1 p 5 } \{ p_{1}p_{5} \} { p 1 p 5 } p 4 p_{4} p 4 M D L p a r MDL_{par} M D L p a r M D L n o p a r MDL_{nopar} M D L n o p a r
线段聚类
线段密度
距离函数回顾
距离函数是三种距离的加权和。
垂直距离主要测量从不同轨迹中提取的线段之间的位置差异
平行距离主要测量从同一轨迹中提取的线段之间的位置差异。在一个轨迹中,两个相邻的线段之间的平行距离始终为零
角度距离测量线段之间的方向差
距离函数的对称性是避免聚类结果的模糊性的重要方法。如果一个距离函数是不对称的,则根据处理顺序的不同可以得到不同的聚类结果。以下是对本文提出的距离函数的对称性的证明:d i s t ( L i , L j ) dist(L_{i},L_{j}) d i s t ( L i , L j ) d i s t ( L i , L j ) = d i s t ( L j , L i ) dist(L_{i},L_{j})=dist(L_{j},L_{i}) d i s t ( L i , L j ) = d i s t ( L j , L i ) d i s t ( L i , L j ) dist(L_{i},L_{j}) d i s t ( L i , L j ) L i L_{i} L i L j L_{j} L j d i s t ( L i , L j ) dist(L_{i},L_{j}) d i s t ( L i , L j )
基于密度的聚类的概念
设D D D
直线段L i ∈ D L_{i}∈D L i ∈ D ε − ε- ε − N ε ( L i ) N_{ε}(L_{i}) N ε ( L i ) N ε ( L i ) = { L j ∈ D ∣ d i s t ( L i , L j ) ≤ ε } N_{ε}(L_{i})={\{ L_{j}∈D|dist(L_{i},L_{j})≤ε \}} N ε ( L i ) = { L j ∈ D ∣ d i s t ( L i , L j ) ≤ ε }
如果∣ N ε ( L i ) ∣ ≥ M i n L n s |N_{ε}(L_{i})|≥MinLns ∣ N ε ( L i ) ∣ ≥ M in L n s L i ∈ D L_{i}∈D L i ∈ D ε ε ε M M M
线段L i ∈ D L_{i}∈D L i ∈ D ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s L j ∈ D L_{j}∈D L j ∈ D L i ∈ N ε ( L j ) L_{i} \in N_{\varepsilon}(L_{j}) L i ∈ N ε ( L j ) ∣ N ε ( L i ) ∣ ≥ M i n L n s |N_{ε}(L_{i})|≥MinLns ∣ N ε ( L i ) ∣ ≥ M in L n s
线段L i ∈ D L_{i}∈D L i ∈ D ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s L j ∈ D L_{j}∈D L j ∈ D L j , L j − 1 , ⋅ ⋅ ⋅ , L i + 1 , L i ∈ D L_{j} , L_{j−1}, · · · , L_{i+1}, L_{i} ∈ D L j , L j − 1 ,⋅⋅⋅, L i + 1 , L i ∈ D L k L_{k} L k ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s
如果有一个线段L k ∈ D L_{k}∈D L k ∈ D L k L_{k} L k ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s L i L_{i} L i L j L_{j} L j L i ∈ D L_{i}∈D L i ∈ D ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s L j ∈ D L_{j}∈D L j ∈ D
一个非空的子集C ⊆ D C⊆D C ⊆ D ε 和 M i n L n s \varepsilon\ 和\ MinLns ε 和 M in L n s C C C
连通性:∀ L i , L j ∈ C ∀L_{i},L_{j}∈C ∀ L i , L j ∈ C L i L_{i} L i ε \varepsilon ε M i n L n s \ MinLns M in L n s L j L_{j} L j
极大性:∀ L i , L j ∈ D ∀L_{i},L_{j}∈D ∀ L i , L j ∈ D L i ∈ C L_{i}∈C L i ∈ C L j L_{j} L j L i L_{i} L i ε 和 M i n L n s ε\ 和\ MinLns ε 和 M in L n s L j ∈ C L_{j}∈C L j ∈ C
密度可达性是直接密度可达性的传递闭包。
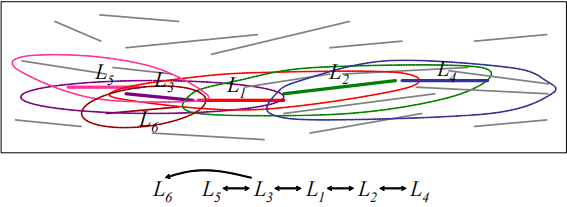
考虑下图中的线段。设 M i n L n s MinLns M in L n s ε − ε- ε −
L 1 、 L 2 、 L 3 、 L 4 和 L 5 L_{1}、L_{2}、L_{3}、L_{4}和L_{5} L 1 、 L 2 、 L 3 、 L 4 和 L 5 L 2 L_{2} L 2 L 3 L_{3} L 3 L 1 L_{1} L 1 L 6 L_{6} L 6 L 1 L_{1} L 1 L 1 L_{1} L 1 L 4 L_{4} L 4 L 5 L_{5} L 5
观察
线段由于同时具有方向和长度,因此具有一些与基于密度的聚类相关的有趣特征:
线段的ε ε ε
一个短线段可能会大大降低聚类质量。一个线段的长度代表其方向强度,即如果一个线段较短,则它的方向强度较低。这意味着,如果其中一个线段非常短,那么无论实际的角度如何,角度距离都很小。l 2 l_{2} l 2 L 1 L_{1} L 1 L 2 L_{2} L 2 L 3 L_{3} L 3 L 1 L_{1} L 1 L 3 L_{3} L 3 c o s t n o p a r cost_{nopar} cos t n o p a r
聚类算法
本文所提出的基于密度的线段聚类算法:给定一个线段集合D D D ε ε ε M i n L n s MinLns M in L n s O O O
该算法与D B S C A N DBSCAN D BSC A N C i C_{i} C i P T R ( C i ) = { T R ( L j ) ∣ ∀ L j ∈ C i } PTR(C_{i}) ={\{ TR(L_{j})|∀L_{j}∈C_{i} \}} PTR ( C i ) = { TR ( L j ) ∣∀ L j ∈ C i } T R ( L j ) TR(L_{j}) TR ( L j ) L j L_{j} L j ∣ P T R ( C i ) ∣ |PTR(C_{i})| ∣ PTR ( C i ) ∣ C i C_{i} C i
最初,假定所有的线段都是未分类的。随着算法的进行,它们被分为簇或噪声。该算法包括如下三个步骤:
第一步(第1∼12行)L L L ε ε ε L L L N ε ( L ) N_{ε}(L) N ε ( L )
第二步(第17∼28行)E x p l a n d C l u s t e r ( ) ExplandCluster () E x pl an d Cl u s t er ( ) Q Q Q Q Q Q
第三步(第13∼16行)
时间复杂度分析: 如果使用空间索引,该算法的时间复杂度为O ( n l o g n ) O(nlogn) O ( n l o g n ) n n n ( ≥ 2 ) (≥2) ( ≥ 2 ) O ( n 2 ) O(n^{2}) O ( n 2 ) ε ε ε n × (一次 ε − 邻域查询的时间复杂度) n×(一次ε-邻域查询的时间复杂度) n × (一次 ε − 邻域查询的时间复杂度) 该算法可以很容易地进行扩展,以支持带有权重的轨迹。例如,一个更强的飓风将有更大的质量,因此需要修改决定一个ε ε ε ∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣
本文的距离函数不是一个度量,因为它不服从三角形不等式,即存在d i s t ( L 1 , L 3 ) > d i s t ( L 1 , L 2 ) + d i s t ( L 2 , L 3 ) dist(L_{1}, L_{3}) > dist(L_{1}, L_{2}) + dist(L_{2}, L_{3}) d i s t ( L 1 , L 3 ) > d i s t ( L 1 , L 2 ) + d i s t ( L 2 , L 3 )
一个集群的代表性轨迹
一个集群的代表性轨迹描述了属于该集群的轨迹分区的整体运动。它可以被认为是集群的一个模式。
我们需要提取关于集群内运动的定量信息,以便领域专家能够理解轨迹中的运动。因此,为了从轨迹聚类中获得充分的实际潜力,绝对需要具有这种代表性的轨迹。
一个具有代表性的轨迹是一个点序列R T R i = p 1 p 2 p 3 ⋅ ⋅ ⋅ p j ⋅ ⋅ ⋅ p l e n i ( 1 ≤ i ≤ n u m c l u s ) RTR_{i}=p_{1}p_{2}p_{3}···p_{j}···p_{len_{i}}(1≤i≤num_{clus}) RT R i = p 1 p 2 p 3 ⋅⋅⋅ p j ⋅⋅⋅ p l e n i ( 1 ≤ i ≤ n u m c l u s ) M i n L n s MinLns M in L n s
为了表示集群的主轴,定义如下平均方向向量:
上述公式将向量而不是它们的方向向量(即单位向量)相加,并对结果进行归一化处理,是一个很好的启发式方法,可以使一个较长的向量对平均方向向量贡献更大的效果。我们计算代表簇中每个线段的向量集合上的平均方向向量。
如上所述,我们计算相对于平均方向向量的平均坐标。为了便于计算,通过[ x ′ y ′ ] = [ cos ϕ sin ϕ − sin ϕ cos ϕ ] [ x y ] \left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{cc}\cos \phi & \sin \phi \\ -\sin \phi & \cos \phi\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] [ x ′ y ′ ] = [ cos ϕ − sin ϕ sin ϕ cos ϕ ] [ x y ] [1] x ^ \hat{x} x ^ φ φ φ X ′ Y ′ X'Y' X ′ Y ′ X Y XY X Y
具有代表性的轨迹生成算法
关于参数值选择的启发式方法
在信息论中,熵与与给定概率分布相关的事件的不确定性量有关。如果所有的结果都是等可能的,那么熵应该是最大的。
作者通过观察发现:在最差的聚类中,∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣ ε ε ε ∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣ ε ε ε ∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣ n u m l n num_{ln} n u m l n n u m l n num_{ln} n u m l n ∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣
熵通过如下公式定义,
H ( X ) = ∑ i = 1 n p ( x i ) log 2 1 p ( x i ) = − ∑ i = 1 n p ( x i ) log 2 p ( x i ) where p ( x i ) = ∣ N ε ( x i ) ∣ ∑ j = 1 n ∣ N ε ( x j ) ∣ and n = n u m l n \begin{gathered}
H(X)=\sum_{i=1}^{n} p\left(x_{i}\right) \log_{2} \frac{1}{p\left(x_{i}\right)}=-\sum_{i=1}^{n} p\left(x_{i}\right) \log_{2} p\left(x_{i}\right) \\
\text { where } p\left(x_{i}\right)=\frac{\left|N_{\varepsilon}\left(x_{i}\right)\right|}{\sum_{j=1}^{n}\left|N_{\varepsilon}\left(x_{j}\right)\right|} \text { and } n=n u m_{l n}
\end{gathered}
H ( X ) = i = 1 ∑ n p ( x i ) log 2 p ( x i ) 1 = − i = 1 ∑ n p ( x i ) log 2 p ( x i ) where p ( x i ) = ∑ j = 1 n ∣ N ε ( x j ) ∣ ∣ N ε ( x i ) ∣ and n = n u m l n
通过模拟退火技术得到时H ( X ) H(X) H ( X ) ε ε ε
选择参数M i n L n s MinLns M in L n s 首先,计算最优ε ε ε ∣ N ε ( L ) ∣ |N_{ε}(L)| ∣ N ε ( L ) ∣ a v g ∣ N ε ( L ) ∣ avg_{|N_{ε}(L)|} a v g ∣ N ε ( L ) ∣ H ( X ) H(X) H ( X ) M i n L n s MinLns M in L n s ( a v g ∣ N ε ( L ) ∣ + 1 ∼ 3 ) (avg_{|N_{ε}(L)|}+1∼3) ( a v g ∣ N ε ( L ) ∣ + 1 ∼ 3 ) M i n L n s MinLns M in L n s a v g ∣ N ε ( L ) ∣ avg|N_{ε}(L)| a vg ∣ N ε ( L ) ∣
通过本文的启发式方法估计的这些参数值是否是真正最优的是不明显的,但该启发式方法提供了一个合理的范围,其中可能存在最优值。可以尝试估计值附近的一些值,并通过目测选择最优值。
实验Experiment
实验设置
数据集: 飓风轨迹数据集和动物运动数据集
聚类质量度量: 平方误差和+噪声惩罚[2]
QMeasure = Total S S E + Noise Penalty = ∑ i = 1 n u m c l u s ( 1 2 ∣ C i ∣ ∑ x ∈ C i ∑ y ∈ C i dist ( x , y ) 2 ) + 1 2 ∣ N ∣ ∑ w ∈ N ∑ z ∈ N dist ( w , z ) 2 \begin{aligned}
\text { QMeasure }=& \text { Total } S S E+\text { Noise Penalty } \\
=& \sum_{i=1}^{n u m_{clus}}\left(\frac{1}{2\left|C_{i}\right|} \sum_{x \in C_{i}} \sum_{y \in C_{i}} \operatorname{dist}(x, y)^{2}\right)+\\
& \frac{1}{2|\mathcal{N}|} \sum_{w \in \mathcal{N}} \sum_{z \in \mathcal{N}} \operatorname{dist}(w, z)^{2}
\end{aligned}
QMeasure = = Total SSE + Noise Penalty i = 1 ∑ n u m c l u s ⎝ ⎛ 2 ∣ C i ∣ 1 x ∈ C i ∑ y ∈ C i ∑ dist ( x , y ) 2 ⎠ ⎞ + 2∣ N ∣ 1 w ∈ N ∑ z ∈ N ∑ dist ( w , z ) 2
其中,N \mathcal{N} N
实验结果
飓风跟踪数据的结果
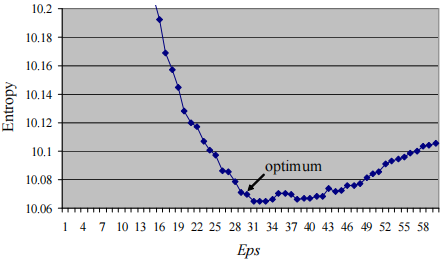
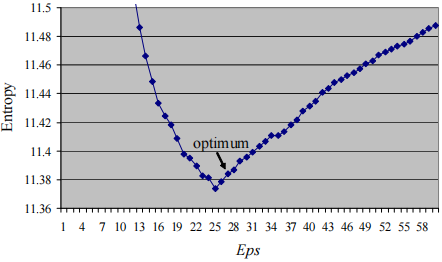
下图显示了ε ε ε ε = 31 ε=31 ε = 31 a v g ∣ N ε ( L ) ∣ = 4.39 avg|N_{ε}(L)|=4.39 a vg ∣ N ε ( L ) ∣ = 4.39 ε = 31 ε=31 ε = 31 M i n L n s = 5 ∼ 7 MinLns=5∼7 M in L n s = 5 ∼ 7 ε = 30 ε=30 ε = 30 M i n L n s = 6 MinLns=6 M in L n s = 6 ε = 30 ε=30 ε = 30 ε = 31 ε=31 ε = 31
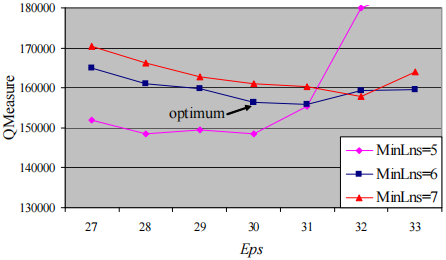
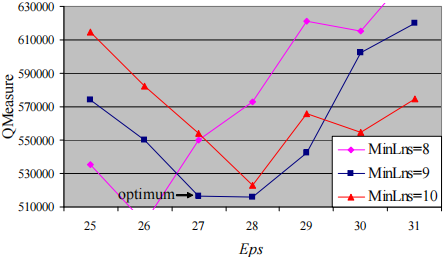
下图显示了ε ε ε M i n L n s MinLns M in L n s M i n L n s = 6 MinLns=6 M in L n s = 6 M i n L n s = 5 MinLns=5 M in L n s = 5 M i n L n s MinLns M in L n s M i n L n s = 6 MinLns=6 M in L n s = 6 ε ε ε
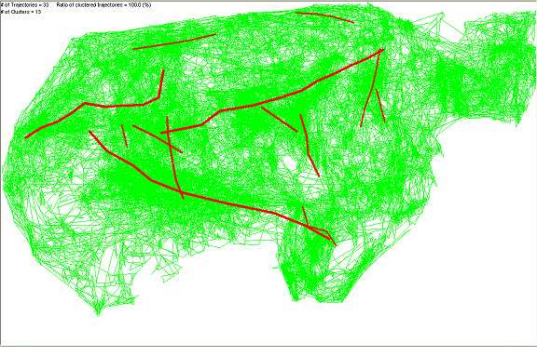
下图显示了使用最优参数值进行的聚类结果。其中,绿色的细线表示轨迹,粗的红色线表示代表性轨迹。
动物运动数据的结果
1993年的麋鹿运动
下图显示了ε ε ε ε = 25 ε=25 ε = 25 a v g ∣ N ε ( L ) ∣ = 7.63 avg|N_{ε}(L)|=7.63 a vg ∣ N ε ( L ) ∣ = 7.63 ε = 27 ε=27 ε = 27 M i n L n s = 9 MinLns=9 M in L n s = 9 ε = 27 ε=27 ε = 27 ε = 25 ε=25 ε = 25
下图显示了ε ε ε M i n L n s MinLns M in L n s
下图显示了使用最优参数值进行的聚类结果。
1995年的鹿运动
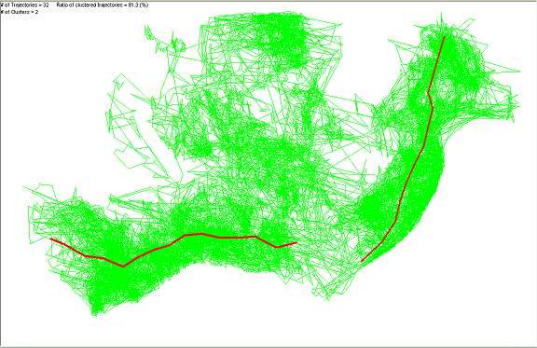
下图显示了使用最优参数值(ε = 29 和 M i n L n s = 8 ε=29和MinLns=8 ε = 29 和 M in L n s = 8
参数值的影响
如果使用更小的ε ε ε M i n L n s MinLns M in L n s ε ε ε M i n L n s MinLns M in L n s
讨论Discussion
该算法的一些可能拓展:
可扩展性: 支持无向的或加权的轨迹,使用简化角距离来处理无向轨迹,使用ε ε ε 参数不敏感性: 使该算法对参数值更不敏感。如将O P T I C S OPTICS OPT I CS 效率: 通过使用索引来进行ε ε ε 运动模式: 扩展该算法以支持各种类型的运动模式,特别是圆周运动。该扩展可以通过增强生成一个具有代表性的轨迹的方法来实现。时间信息: 在聚类过程中考虑时间信息。